今日は「RIJ(へき地尺度)と病院経営」に関する研究解析で、大きな学びがあった。
RIJスコアを四分位で分けた単変量解析では、明確に有意差が出た。へき地になるほど経営が悪化している――そんな仮説に“統計的な後ろ盾”が得られたかに見えた。
しかし――多変量解析では、その関連が消えてしまった。
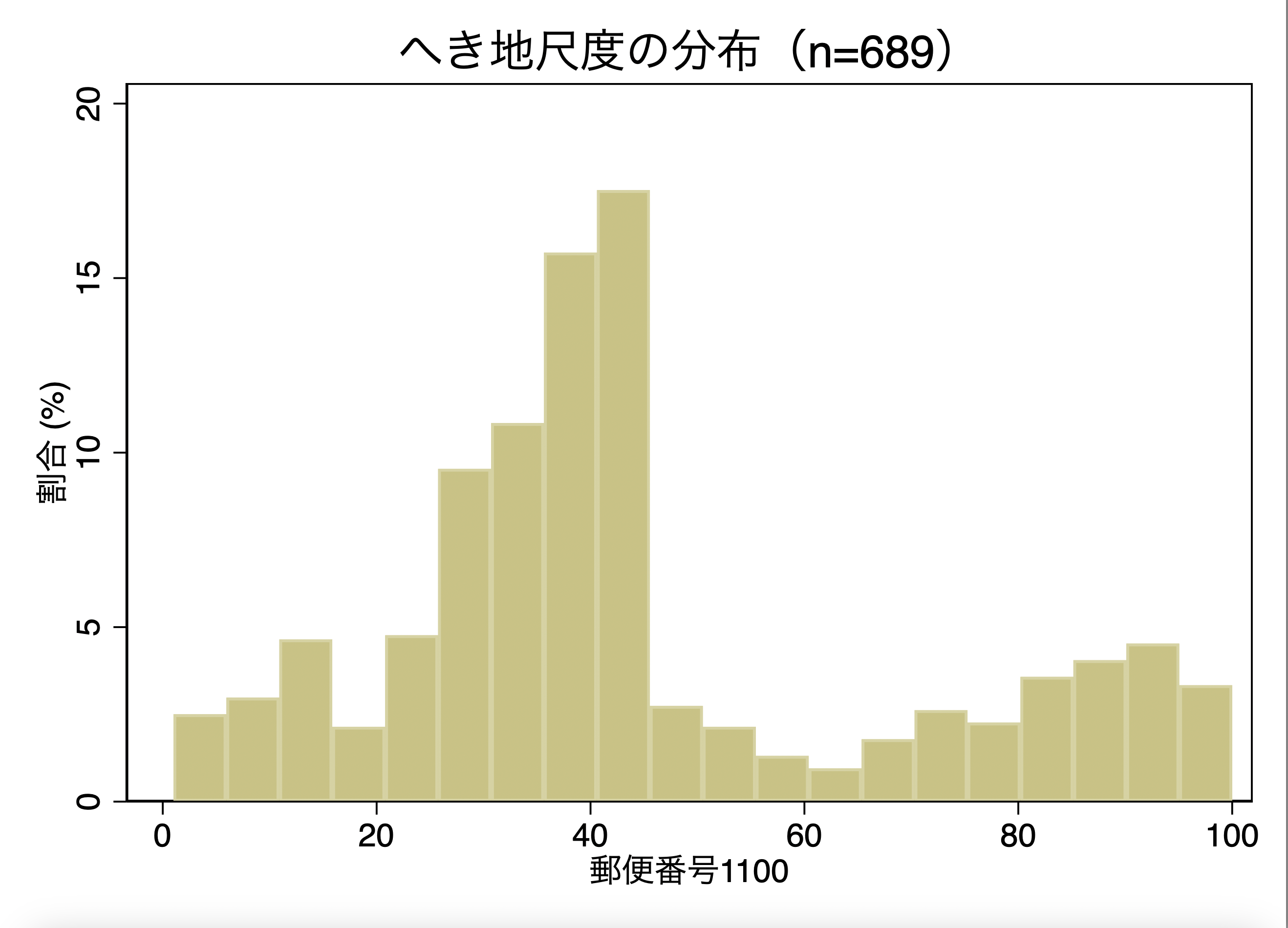
一見すると「仮説が否定された」ように感じるが、実はここに大きな意味がある。へき地性は「病院規模」や「稼働率」などと密接に結びついている。へき地であること自体より、そこで起こる構造的制約(例:人手不足による稼働率低下)の方が、経営悪化の本質だったということだ。
つまり、**単変量解析は「きっかけ」**を与え、**多変量解析は「真因」**を探る手段。
有意差が「消える」ことは、むしろ次の問いの始まり。
どの変数がその影響を媒介しているのか。
どの要因を整えれば政策的に改善が可能なのか。
「統計は、問いを閉じるためではなく、問いを深めるためにある」。
そんな当たり前を、今日はあらためて実感した。
💡今後どのような場面で使い分けるべきか?
◉ 単変量解析が有効な場面(Exploratory):
- 仮説生成・全体傾向の把握
- プレゼン資料や政策提言の導入部に「視覚的インパクト」を出したいとき
- 大量の変数を扱うときの「スクリーニング的用途」
- 学生指導で統計の「第一歩」として使うとき
🧭例:「この変数、ざっくりグループで比べたらどうなってる?」
◉ 多変量解析が有効な場面(Confirmatory):
- 因果関係を検証したいとき(交絡因子の調整)
- 論文における主要なエビデンス提示(adjusted ORやβ係数)
- 「独立した影響力」を問う政策論文・報告書など
- 知見を一般化可能な形で示す必要があるとき
🧭例:「この変数、他の因子を調整したあとでも影響してる?」
📎 使い分けの鉄則(シンプルに)
| 目的 | 手法 | 例 |
|---|---|---|
| 仮説を立てる | 単変量解析 | クロス集計、ANOVAなど |
| 仮説を検証する | 多変量解析 | 回帰分析、ロジスティック回帰など |
| 因果の筋道を描く | 構造モデル or 交互作用・媒介分析 | SEM、path分析、交互作用項など |


