日々勉強です。
統計解析の多くは、Xが増えるとYも直線的に変化するという「線形モデル」を前提としている。
だが現実の臨床データはそんなに素直ではない。
たとえば、へき地スコア(RIJ)と病院の医業赤字リスクの関係。「田舎になるほど赤字になるのか?」という問いに、線形モデルでは答えられないことがある。
なぜなら、リスクは一定レベルを超えて初めて急激に増える可能性があるからです。
そこで使えるのが──スプライン解析(Spline Analysis)でした。
🔍 スプライン解析とは?
- 連続変数(例:年齢、スコア)とアウトカムの“曲線的な関係”を可視化できる
- 特に医療政策や臨床研究で「どこからリスクが増え始めるか?」というしきい値の探索に強い
- 多くの場合、「restricted cubic spline(制限付き三次スプライン)」を使う
📊 スプライン解析の例:RIJスコアと赤字リスク
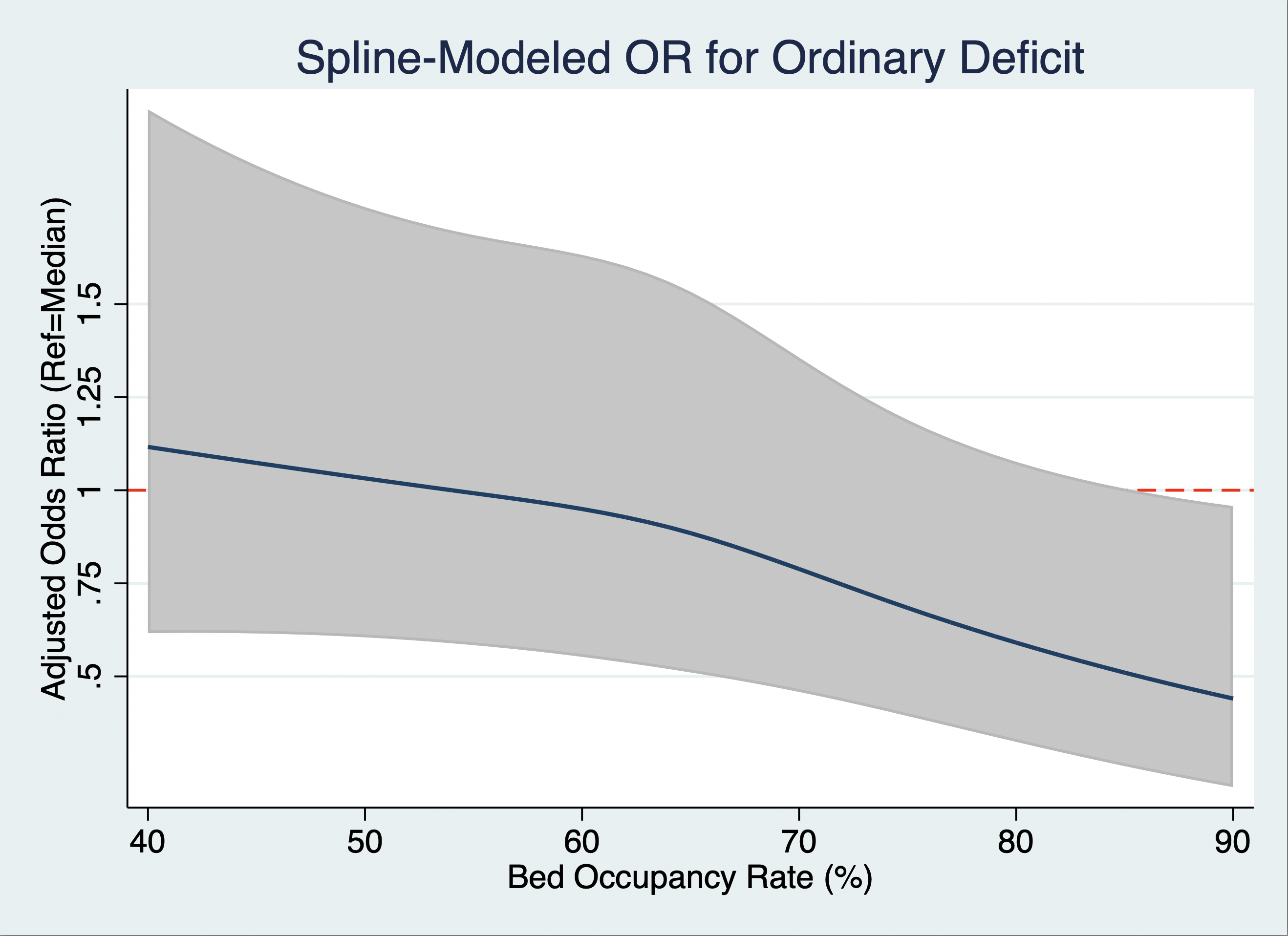
下の図では、RIJスコア(へき地度)が60を超えるあたりから、急激に赤字リスク(オッズ比)が上昇することが示されている:
📈
- 青線:オッズ比(Adjusted OR)
- グレー帯:95%信頼区間
- 横軸:RIJスコア、縦軸:赤字リスク(OR)
ポイントは、「ある地点から急にリスクが跳ね上がる」という非線形性。
これを「1.0」「1.5」「2.0」などのカットオフで無理に区切ってしまうと、本質が見えなくなる。
✅ 学びまとめ
| 単純な線形モデル | スプラインモデル |
|---|---|
| XとYは直線的関係 | XとYは曲線的関係もOK |
| 見逃すリスクが高い | 関係の形状まで可視化 |
| シンプルだが粗い | 複雑だが示唆が深い |
✏️ 実務での活かし方
- へき地政策で「支援が必要なレベル」を定量的に可視化
- 医療者の年齢・労働時間・収入などとバーンアウトの非線形関係をモデル化
- 投薬量と副作用、手術時間と転帰などの閾値探索にも応用可
坂口先生の研究のように、「単に有意かどうか」ではなく、「どのように関係しているか」に目を向けること。
それが、臨床と政策の橋をかける統計的視点だと実感しています。


